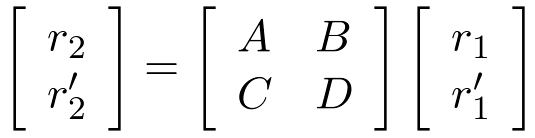Matrix Description of Ray Propagation
J. C. Daly
October 1, 2016
As a paraxial ray propagates through an optical system we want to determine its
position and slope relative to the optical axis.
A 2x2 matrix is used to calculate ray position and slope based on the ray position and slope
at a previous position. The system is broken down into elements that can be describes
using simple ABCD matrices.
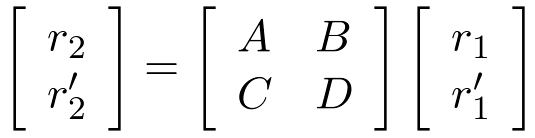 | (1) |

Figure 1 Three common elements of ray propagation are shown; (a) propagation through a space, (b)
propagation through a thin lens, and (c) propagation through a spherical dielectric interface.
|
Propagation through space
Propagation through space is shown in Figure 1(a) and is described by the following matrix equation.
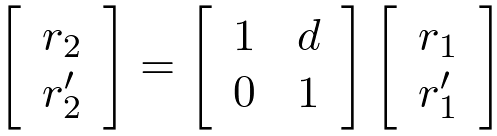 | (2) |
The slope of a ray propagating through space does not change.
r '2 = r '1.
The distance of the ray from the optical axis changes by an amount proportional to its slope and the
distance traveled.
Propagation through a thin lens
Ray propagation through a thin lens is shown in Figure 1(b) and described by the following matrix
equation.
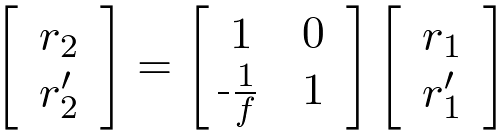 | (3) |
When a ray propagates through a thin lens, its distance from the optical axis does not change.
A thin lens makes a negative change in the ray's slope by an amount proportional to the distance
of the ray from the optical axis. The change in slope is the ray displacement from the axis divided by
the negative of the lenses focal length. This defines focal length. Horizontal rays are bent toward
the axis and pass through it at a distance from the lens equal to the focal length.
Propagation through a spherical dielectric interface
The physical nature of lenses can be understood by considering the propagation of rays through
a spherical dielectric interface as shown in Figure 1(c) and in Figure 2. Propagation through
a spherical dielectric interface is described by the following matrix equation.
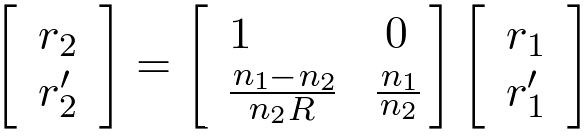 | (4) |
where n1 us the index of refraction on the left side of the interface
and n2 is the index of refraction to the right of the interface.
Equation 4 can be obtained by considering Figure 2 showing the spherical dielectric interface.
The distance of the ray from the optical axis does not change at the interface, but the slope does.
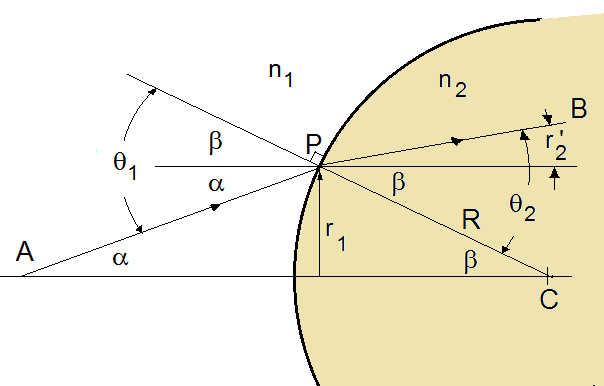
Figure 2 Ray propagation through a spherical dielectric interface is shown.
A ray propagates from A to P in one medium and from P to B in a second medium.
R is the radius of curvature of the spherical interface. |
A ray propagates from A to P in medium 1 and from P to B in medium 2. In medium 1 the ray slope is,
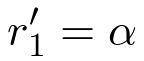 | (5) |
Since for paraxial rays (small angles) tan(b) = b,
 | (6) |
Also
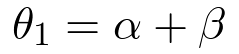 | (7) |
The slope in medium 2 is,
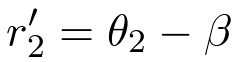 | (8) |
From Snell's law for paraxial rays,
 | (9) |
It follows that,
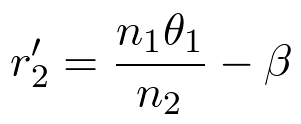 | (10) |
Combining Equations 7 and 10,
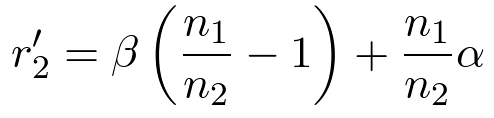 | (11) |
Rearranging terms and using Equations 5 and 6,
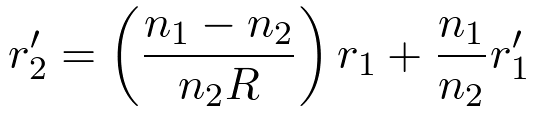 | (12) |
Equation 12 is included in Equation 4.