Reflected Waves

J. C. Daly
October 24, 2016


Figure 1
A light wave traveling through an medium with an index of refraction n1 is incident on the surface of a second medium with an index of refraction n2. Some of the light is reflected and some is transmitted into the second medium. The interface is at z = 0, as shown in Figure 1.

Let's use the magnetic field intensity H instead of the magnetic flux density B.

Recall that H is proportional to the magnetic flux density B.


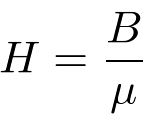
(1)
where u is the permeability of the medium. The the magnetic flux density of the wave propagating in the positive z direction is

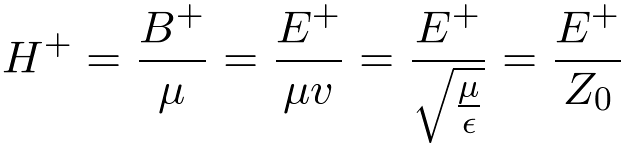
(2)
Also, where

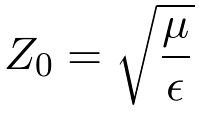
(3)
is the characteristic impedance of the medium.

The electric field is the sum of a wave traveling in the positive z direction and a wave traveling in the negative z direction.


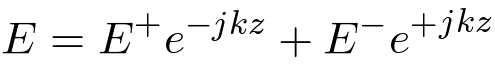
(4)
The magnetic field also consists of waves traveling in the positive and negative directions.

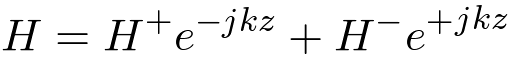
(5)

Since the interface is at z = 0 and l is the distance from the interface, in medium 1.


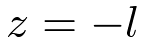
(6)
Changing variables, writing Equations 4 and 5 in terms of the distance from the interface, letting z = -l.

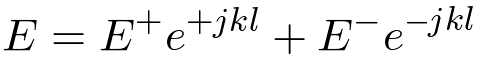
(7)

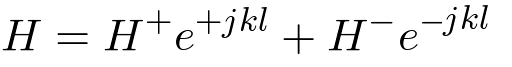
(8)
From Equation 2 it follows that,

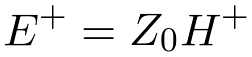
(9)
The equivalent expression for the wave traveling in the negative z direction is,

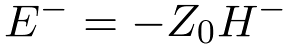
(10)
Recall that the cross product of E and H (E X H) is in the direction of propagation. This results in the minus sign in Equation 10.

At the interface,


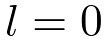
(11)
and from Equation 7 at l = 0,

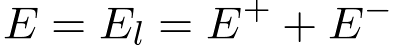
(12)
Where El is the electric field at the interface. Also from Equation 8 the magnetic field at the interface is,

(13)
where Hl is the magnetic field at the interface.

Combining Equations 9, 10, and 13,


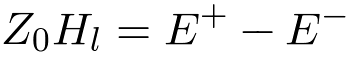
(14)

Add Equations 12 and 14,


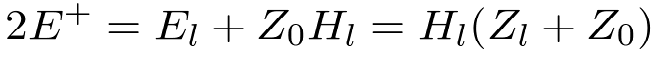
(15)
where Zl, the impedance at the interface is

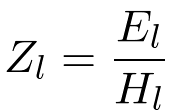
(16)
Subtracting Equation 14 from Equation 12.

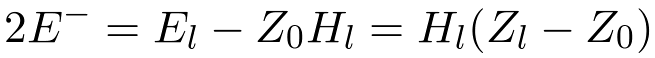
(17)
Solving for E+ and E - and plugging into Equation 7,

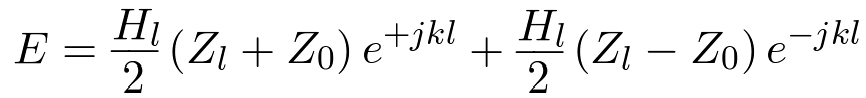
(18)
Similarly using equations 8, 9, and 10

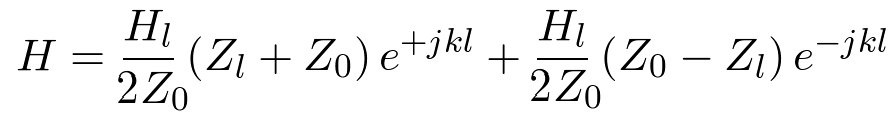
(19)
Since

We can write Equations 18 and 19 as

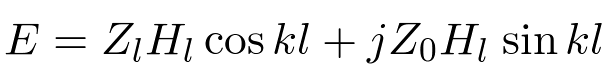
(20)

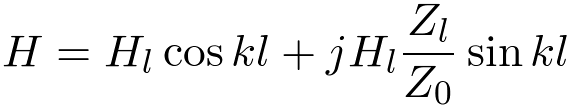
(21)
Matrix Description

Since   Hl Zl = El,   Equations 20 and 21 can be written in matrix form,


(22)
where the subscript "1" refers to the fields at the interface between medium 1 and medium 2. Subscript "2" refers to the interface between medium 2 and medium 3. For the case where the thickness of medium 2 is a quarter wave length.

(23)
This results in the following transfer matrix equation.

(24)
where Z1 is the characteristic impedance of medium 1.

(24)

(25)

(26)
From the first row of Equation 26 and that the electric field is continuous across the boundary it follows that,

(27)
From the second row of Equation 26 and that the magnetic field is continuous across the boundary it follows that,

(28)
Since Z0 / Z3 = n3 / n0 it follows from Equation 28 that,

(29)
Subtracting Equation 29 from Equation 27,

(30)
The reflected electric field Er is zero when,

(31)